Several years ago, I read the book The Signal and the Noise. The book focuses on how to make better predictions. In Chapter 9, the author talks about building a chess engine. At the time, this inspired me to create a chess engine in Python. I had absolutely no idea what I was doing, but it was a great learning experience.
Fast forward to now, I came across a chess engine challenge on YouTube. The goal of the challenge is to make a bot-sized engine (challenge Github page) in C#.
In this post, I will:
- Provide an overview of the basic chess engine capabilities that I added (e.g., min/max, lookup table)
- Walk through my turtle strategy
- Test against Stockfish
Feel free to check out my code. You are also free to use my code as a starting point for your own entry. If so, let me know in the comments below how you improved the engine.
Basic Chess Engine Capabilities
One of the great parts about this challenge is that it forced me to learn some basics of chess engine development. In this section, we will cover the basics of running and optimizing the chess engine:
The basics:
- MinMax
- Alpha-Beta Pruning
- Hash/Lookup table
MinMax
My engine is built on the MinMax algorithm (as are many chess engines).
The MinMax algorithm is a fundamental concept in game theory (particularly for two-player zero-sum games). The basic idea is that a player will try to maximize their position and the opponent will attempt to minimize. The algorithm considers all possible moves and outcomes, alternating the evaluation between maximizing the player’s potential gain and minimizing the opponent’s potential gain at each level of the tree. This process ultimately leads to the selection of the best move that maximizes the player’s chances of success, even in the presence of a knowledgeable and strategic opponent.
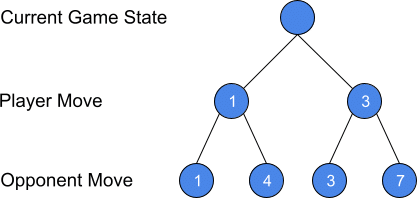
For example, in the graphic below, the current game state is represented as the root node. The player has two options, left or right. To decide which option, the player considers each of the opponents possible moves after the player plays. The opponent will have four possible moves. The evaluation function calculates the board at the end of each of the opponent’s moves. The opponent will always seek to minimize the player’s position. In this case, the opponent would select the 1 or 3 nodes. Therefore, the player should choose the right, because 3 > 1. Note that this is worst case. If the opponent makes a mistake with their move selection, the best case is 7.
Alpha-Beta Pruning
The MinMax algorithm evaluates all potential moves. In the example above, at a depth of 2 (player move and opponent move), we had to evaluate 4 nodes. If we add one more depth, we will increase to 8 nodes. For this game, the number of nodes that we need to evaluate is 2^depth (2^3 = 8).
For chess, the numbers are significantly larger. At the start of the game, white and black each have 20 possible moves. Therefore, a depth of 2 requires evaluation of 20*20=400. Adding just one more level (depth=3), the algorithm would need to evaluate 8,000 nodes.
For my bot, once I had MinMax running, I could barely run at a depth greater than 1. The algorithm was too slow, and I kept running out of time (the challenge gives each bot just 1 minutes of playing time). As I researched ways to speed up a chess engine, the top result was Alpha-Beta Pruning. This significantly improved my result, allowing me to increase the depth to 3.
It took me a long time to understand how alpha-beta pruning works. Hopefully, my explanation below is helpful.
Basically, alpha-beta pruning allows us to skip evaluating certain nodes. This works because the player and opponent are working against each other. As discussed above, the player is always trying to maximize their position and the opponent is minimizing the player’s position.
For a simple example, let’s take the figure from above. We will replace the last node with a ?. We have not calculated the node, and we can skip calculating the node, because it doesn’t matter.
The final node could be any number. Let’s go through the 3 possibilities: >1, <1, and =1.
- = 1: Doesn’t matter which one the opponent picks, they are the same.
- > 1: The minimizer will never pick it. The opponent will take the 1, because it minimizes the player’s position.
- < 1: The maximizer will never pick it. If the number is -700, the minimizer would obviously pick it instead of the 1. However, the player is then choosing between -700 and 3. The player would much prefer the 3.
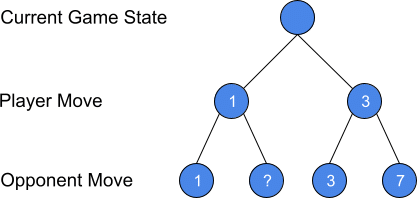
To implement alpha-beta pruning, we just need to add two variables: alpha and beta. At any point, we will stop evaluating nodes if beta <= alpha. In the diagram above, this is the 1 (beta) < 3 (alpha). We know the player will never pick anything less than the 3.
When we start, we set alpha to -infinity and beta to infinity. Therefore, beta <= alpha is false. During the minimize phase, we update the beta score by taking the minimum of either the previous beta or the currently evaluated score. For example, if the 3 node is the first node we evaluate, then we would take min(3,beta). Since beta starts at infinity, min(3,infinity) is 3. Therefore, we update beta to 3. Now, when we evaluate the 7, min(3,7)=3. Beta doesn’t change. The minimizer chooses the 3. Now the algorithm starts on the next branch. Alpha is updated to 3. The player cannot do any worse than a 3. The 1 node is evaluated. 1 <= 3 (alpha). Therefore, the algorithm stops searching.
As mentioned above, if the number of possible moves is m and the depth is d, the total number of nodes we need to evaluate is m^d. Alpha-beta pruning allows us to reduce the number of nodes we need to evaluate from m^d to approximately m^(d/2). If m=20 and d=3, no pruning is 8,000 evaluations, pruning is 89 evaluations!
Lookup Table
Another method to speed up calculation is to not recalculate something that we already know. For example, if we have an arbitrary board position P that results in a score of 5, we don’t want to run the evaluation every time the board looks exactly like P. Instead, we want to store that board and score. To do that, we create a hash of the board. We use the hash as the dictionary key, and we associate the key with the score value. Therefore, before we do the calculation, we hash the board and check whether the hash exists in the dictionary. If yes, we simply return the value from the dictionary. If no, then we calculate and store the calculated value in the dictionary.
In the case of this challenge, the base challenge code includes a number of functions for working with the board, including a hash function (Zobrist hash).
Optimization
One of the parts that I love about this challenge is the fact that there are code limits. The purpose of this challenge is to create a bot-sized chess bot. To enforce the bot-sized chess requirement, the challenge uses Microsoft Code Analysis to count the number of tokens. A token is any keyword, identifier, operator, or punctuation. The bot can have no more than 1024 tokens.
My code is currently at 1012 tokens. There are a few more enhancements that I would like to add (see the next step section below). However, if I want to add anything, I will need to simplify my existing code. One potential area is the min/max functions. I have two different functions that are mostly the same code. The other potential optimization I can make is to review each of the loops in more detail. When the computation complexity is O(m^d), loops add up quickly.
Turtle Strategy
For this challenge, the creator encourages creativity. In his version, he created an EvilBot. This bot has no depth search and simply tries to either mate in 1 or take out the highest value piece. Otherwise, it plays randomly.
My approach to this challenge was to create a TurtleBot. My engine will focus on slow and steady development of the board. My goals are to:
- Control the center of the board
- Avoid placing queen, bishop, and rook on the edge of the board
Control the Center
The first goal of the engine is to control the center. When I first learned to play chess, I learned that it was important to control the middle of the board. Someone described the middle as the hill you must capture. If your pieces are in the middle, they can attack anywhere. In addition, if you want to move pieces across the board, you often need to go through the middle. Therefore, in my evaluation, I count the number of white pieces and black pieces and multiply the difference by 3.

Knight on the Rim is Dim
There is a saying in chess that a “knight on the rim is dim.” This is based on the fact that a knight normally has 8 moves. However, if you place the knight on the edge, you cut the number of moves in half (even more if the knight is in a corner). Similar rules apply to bishops and queens (although maybe not as severe). Therefore, we reduce the score if the knight, bishop or queen is on the edge of the board.
Test Against Stockfish Chess Engine
Once I had my basic algorithm up and running, I could easily beat the EvilBot (winning approximately 86%, 14% draws, and no losses). Therefore, I wanted to train against something more difficult. I added a Stockfish bot. Stockfish is an open source chess engine.
To create, I added Stockfish.NET. I originally added as a submodule. I originally did not intend on making any changes. However, I ran into compile errors with some of the test code. Therefore, I removed the submodule, copied the code into my repo and deleted the problematic test code (I didn’t need it anyway). I then replace the MyBot vs MyBot option in the UI with MyBot vs StockfishBot.
This was definitely a more difficult test. In my initial test, I lost a lot. Out of 43 games, I won once and lost 25 times with 17 draws.
Conclusion: Next Steps for our Chess Engine
There is a lot more that I want to do with my engine. First, my scoring values were subjectively picked. Although based on my experience, I have no idea if they are correct. Therefore, I want to run some basic ML to see if I can improve the weighting of the different factors. Second, I want to go through the code to see where I can simplify, potentially increasing the depth I can search. Third, I want to dynamically change the depth based on the amount of time that I have and the number of pieces. I don’t want to lose the game still having 50 seconds left.





One Comment