Recently, my son was sick. While at the doctor’s office, I noticed that Deal or No Deal was playing on the TV. It was a nice throwback. I remember watching the show when it first came out. As I watched, I was frustrated that the contestant’s friends kept pressuring her into turning down increasingly higher offers, only for her to eventually accept a lower offer. This made me wonder more about the best strategy to play the game. Therefore, I decided to do some analysis and simulation.
Understanding the Data
I started with research, and I came across this article. Most importantly, the author of the article watched over 100 episodes of Deal or No Deal to create a helpful dataset. The author’s research would have been sufficient, but I enjoyed running my own research against the data to understand what was happening.
Throughout this post, we will be using the data from the dataset. Here is the code that we use to import the data.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import scipy
import random
# Load the data
data = pd.read_csv("dond_game_data.csv")Most interesting, was this graphic showing the relationship between different variables:
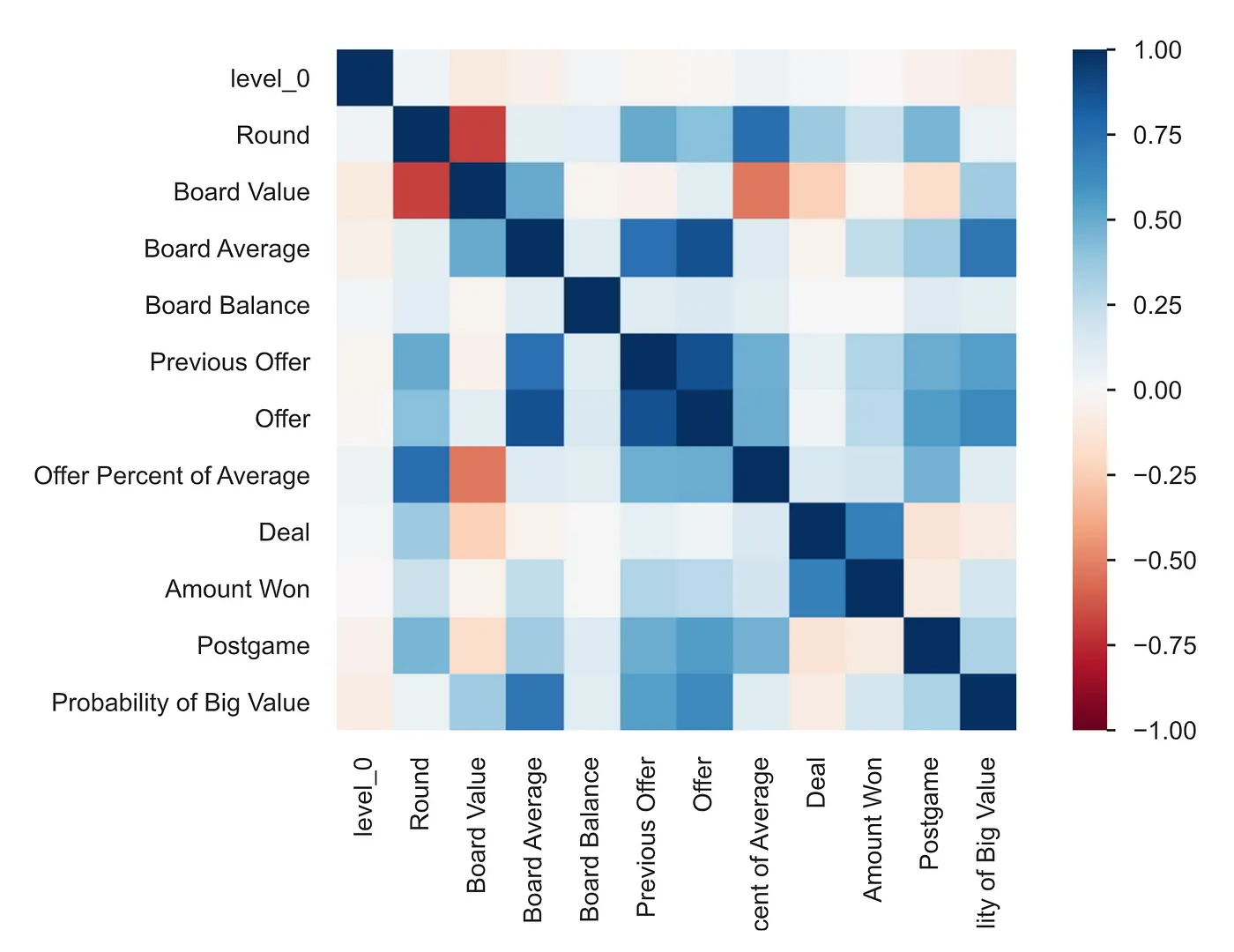
The strongest negative relationship is the round and board value. This is not surprising since you open cases each round, reducing the total value of the board. However, the second most interesting relationship is the round and offer percentage of board average.
Estimating the Offer
Using the following code, I plotted the offer percentage against the round using a box chart.
# Visualize the Offer Percent vs the Round
sns.boxplot(x="Round", y="Offer Percent of Average", data=data)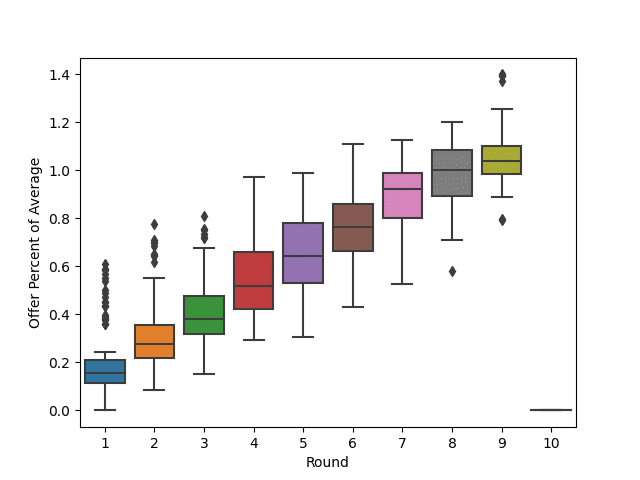
This demonstrates a relatively linear relationship between the round and the offer percentage. We can see the linear relationship more clearly using regression.
# Visualize the Offer Percent vs the Round
sns.regplot(x="Round", y="Offer Percent of Average", data=data)
# Find the linear regression equation
slope, intercept, r, p, sterr = scipy.stats.linregress(x=data['Round'],
y=data['Offer Percent of Average'])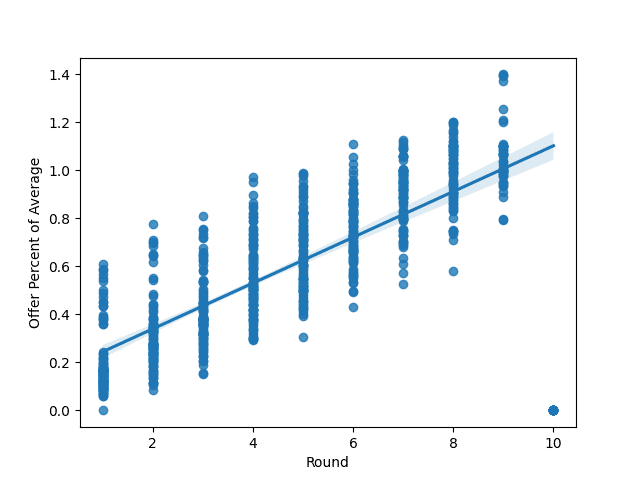
Based on the linear regression, we can estimate the offer percentage by the equation:
y = 0.09x + 0.148
In short, this means you should hold out for an offer in the later rounds.
The Theory of the Offer
There are a number of theories online as to why the offers are so low at the beginning and so much higher toward the end. One theory is that early in the game, the show has leverage over the contestant and can offer the low amount. Some contestants will accept the offer. The theory suggests that toward the end of the game, the show is trying to manage risk. Therefore, the show increases their offer to encourage the contestant to accept the offer instead of the show risking a million dollar payout.
This theory has some support in the data. If you look at the average winnings across all 100 games, you see that the average is $112,705. This is lower than the average if every contestant played to the end of every game (~$136,000).
Counterintuitively, the offer percentage is lower if there are more cases over $100,000. In the plot below, if there are no cases over 100k, the mean offer is around 90%, whereas if the probability of a large case is 60%, the offer is closer to 75%. Initially, you would think that if the show was managing risk, they would give a higher offer to end the game. However, this actually makes sense (depending on the round). A higher number of large cases means that there is a higher probability that the next case opened will be a big case. Therefore, you want to offer a lower amount in the hopes that the contestant will open one more case.
# Let's look at the probability of amount greater than 100k vs the offer percentage
current_data = data[data['Round']==6]
sns.boxplot(x="Probability of Big Value", y="Offer Percent of Average", data=current_data)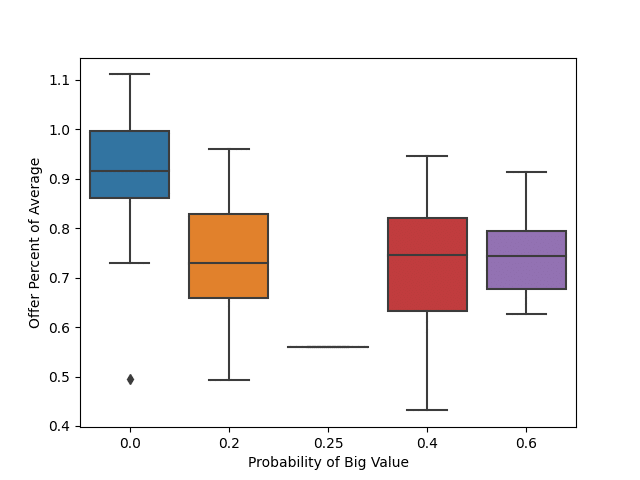
The theory makes sense. However, I have an additional theory that may explain some of the noise in the data. The show doesn’t exist for the contestants. It exists for the viewers. Therefore, I think that some of the offers are driven by drama. The show wants to create engaging stories that keep the viewer watching.
I think the low offers at the beginning encourage the contestant to stay in. Throughout the rounds, the host asks questions of the contestant that allow the viewer to develop an emotional connection. The viewer feels vested in the game. To encourage the contestant to stay in, and to build the connection, the show makes unreasonably low offers in the beginning.
For example, in one game (Game ID 0026, round 1), the average case on the board was worth $155,669. Yet the show only offered $18,000. Initially, this may seem great for the show if the contestant accepts, but in reality it is probably not great for the show. If a contestant exits on round 1 with $18,000, the viewers will not have any emotional attachment to the contestant. In addition, it is not exciting for someone to only win $18,000.
Based on the low, early offers, almost no one accepts the offer before round 6. After round 6, the accepted offers decrease until round 10 (the end).
# Number of deals by round
deals = data[data['Deal']==1]
sns.countplot(x="Round", data=deals)Average Case Value by Round
If we plot the mean and median of the data, the average case value on the board is relatively stable around $146,000 through round 6. According to the data, starting in round 6, the average case value increases linearly through round 9. However, the chart could be misleading. The number of games drops by half through round 9 due to contestants accepting offers. If we instead simulate games through round 9, the mean rises to approximately $154,000 while the median drops to $15,000.
# Average amount of case on the board by round
rounds = [1,2,3,4,5,6,7,8,9]
average = []
median = []
for curr_round in rounds:
round_data = data[data['Round']==curr_round]
average.append(np.mean(round_data['Board Average']))
median.append(np.median(round_data['Board Average']))
plt.plot(rounds, average, label="Mean")
plt.plot(rounds, median, label="Median")
plt.xlabel("Round")
plt.ylabel("Case Value")
plt.legend()
The drop in the median value makes sense due to the relatively few large values on the right side of the prize chart. The starting median value is $875.
| 0.01 | 1,000 |
| 1 | 5,000 |
| 5 | 10,000 |
| 10 | 25,000 |
| 25 | 50,000 |
| 50 | 75,000 |
| 75 | 100,000 |
| 100 | 200,000 |
| 200 | 300,000 |
| 300 | 400,000 |
| 400 | 500,000 |
| 500 | 750,000 |
| 750 | 1,000,000 |
Based on the increasing offers and the relatively stable average board value. It would make the most sense, on average, to wait until at least round 9 before accepting an offer. However, working on the average may not work well for all contestants. Some contestants will open a case with $1,000,000, but some will only receive $0.01.
Creating the Deal or No Deal Decision Heuristic
Now that we understand how the game and the offers work, we want to create a heuristic to help us analyze the best possible outcomes. The heuristic depends on what we want to achieve. In my case, my target is better than average. I want my winnings to be greater than or equal to $131,477, which is the starting average.
To achieve this, my first rule is not to accept an offer before round 6. As noted above, the average case value doesn’t change that much through round 6 and the offers are very low. The round 6 offer will only be around 70%.
At the end of round 6, we will have 4 cases remaining on the board (and 5 potential prize values including the case I selected). At this point, we will start looking at our probabilities. We want to minimize the probability of opening a large case. The challenge is balancing this against the average offer percentage. The best case is to get to the final offer, but not at the expense of losing a large value.
We will have three rules to help us decide whether to stop opening:
Rule 1: If the offer is greater than $140,000 and the percentage of cases larger than our offer is greater than or equal to 50%, then we stop. An offer of $140,000 means that we beat the average. There are too many large cases available, and if we open one more case, the chances are high that it will be a case that is higher than our offer.
For example, if at the end of 6, the remaining values are $10,000, $50,000, $100,000, $300,000, and $1,000,000. The average board value is $292,000. If we open another case, it is more likely that we will open one of the big cases. Therefore, we should stop.
Rule 2: If we have an odd number of cases remaining (including our own), then we accept if the offer is below the median. This may initially seem wrong. We are potentially undervaluing the board. However, the reason for this is related to rule 1 above. If the offer is below the median, it means there are more cases that are bigger than the offer than lower.
Rule 3: In all other cases, keep going.
Applying this heuristic and simulating across 5000 games resulted in an average win amount of $273,478.
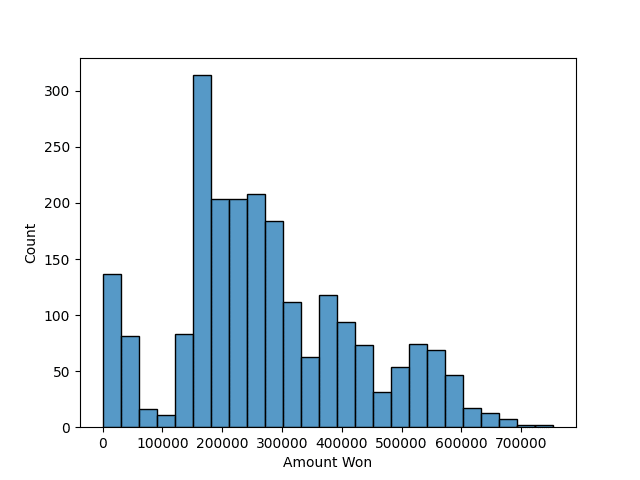
This is significantly better than:
- Playing to the end of the game: $129,714
- Randomly accepting the offer: $120,895
Should You Switch Cases
If the contestant reaches the last round, the contestant is offered the opportunity to switch the case for the remaining case. Should the contestant take this offer? The answer is absolutely not. However, let’s start with the reason why some people think it is a good idea.
The Monty Hall Problem
The idea is based on the Monty Hall problem. In this problem, the contestant is presented with three doors. Only one door has a prize. The contestant selects a door. The host then eliminates one of the remaining doors that doesn’t have the prize. The contestant then has the choice. Do they keep the door they originally selected, or switch? In this case, the contestant should always switch. Why?
When the contestant originally selected their door, they had a 33% chance of picking the prize. They had a 66% chance of not selecting the prize. Most likely they did not pick the door with the prize. The host eliminates a door that does not have the prize. It feels like the choice is 50-50 at this point, because there are two doors remaining, and either door could have the prize. This is deceptive. The probability is actually still 33% that you have the prize, and the remaining door has 66% chance of holding the prize.
Deal or No Deal Is Not the Monty Hall Problem
So why then should the Deal or No Deal contestant not switch. When they selected their case, they had a 1/26 chance of selecting the $1 million case. They had 25/26 chance of not selecting it. Therefore, after opening 24 cases and being left with the one they selected and the one remaining case, the contestant could reason based on the Monty Hall Problem that they should switch because the remaining case has a 25/26 chance of containing the prize.
This is not true. The difference is who opened the cases. If the Deal or No Deal host opened the cases, then definitely switch. However, in the game, the contestant chooses the cases to open. This difference may not feel significant, but it is critical.
The contestant could have selected any case on the board to open. If the million dollar case is still on the board, with every case that they open, the probability of opening the million dollar case increases. By the time we get to round 10, there are only two cases on the board. If the million dollar case is one of those two, the contestant has a 50-50 chance of selecting it.
At this point, if the case they open is not the million dollar case, they have had 24 chances to randomly open the case. This means, the probability of opening the million dollar case was 92% (24/26). 9 out of 10 times, you would have opened the million dollar case by this point. Keep in mind that you could have opened the remaining case at any point. Therefore, it is more likely that you didn’t open the million dollar case, because the million dollar case is not on the board. Instead, it is the one you selected. Don’t switch your case.
Conclusion
What is the practical value of this analysis? Probably not much. The probability of getting to play a Deal or No Deal game is extremely low. However, we had fun working out probabilities and a heuristic as well as developing code to simulate playing games. The code is messy, but below is our full code to test and simulate.
What’s Your Strategy?
Did you find a flaw in my heuristic? Have you simulated your own approach that beats $273,478? Drop a comment below and let me know what you discovered.
Want more posts like this? Get monthly tutorials on Python, probability, game theory, and other fun coding projects delivered straight to your inbox. Sign up for the newsletter and you’ll never miss a post.
import random
import numpy as np
import ast
# Class to manage cases
# Handles the current state of cases, opening cases, and reporting various stats.
class Cases:
# Generates the cases
def __init__(self):
self.cases = {}
possible = [0,1,5,10,25,50,75,100,200,300,400,500,750,1000,5000,10000,25000,50000,75000,100000,200000,300000,400000,500000,750000,1000000]
random.shuffle(possible)
for index in range(26):
self.cases[index] = possible[index]
def __len__(self):
return len(self.cases)
def GetMedian(self):
case_values = list(self.cases.values())
return np.median(case_values)
def GetMean(self):
case_values = list(self.cases.values())
return np.mean(case_values)
# Get the probability of a large case (by default a case greater than or equal to 100k)
def GetLargeProb(self, prob=100000):
case_values = list(self.cases.values())
count = 0
for curr_case in case_values:
if curr_case >= prob:
count += 1
return count/len(case_values)
# Get the stats for the remaining cases
def GetStats(self):
case_values = list(self.cases.values())
case_stats = {}
case_stats["Remaining Values"] = sorted(case_values)
case_stats["Board Average"] = np.mean(case_values)
case_stats["Board Median"] = np.median(case_values)
board_value = 0
big_value_count = 0
for value in case_values:
board_value += value
if value >= 100000:
big_value_count += 1
case_stats["Board Value"] = board_value
case_stats["Big Value Probability"] = big_value_count / len(case_values)
return case_stats
def RemainingCases(self):
return list(self.cases.keys())
def RemainingAmounts(self):
return sorted(list(self.cases.values()))
def OpenCase(self, case_num, verbose=False):
case_value = self.cases[case_num]
self.cases.pop(case_num)
if verbose:
print("Case " + str(case_num) + " contained " + str(case_value) + ".")
return case_value
def OpenRandomCases(self, num=1, verbose=False):
# Opens a random number of cases specified by num
case_nums = list(self.cases.keys())
random.shuffle(case_nums)
for index in range(num):
caseValue = self.OpenCase(case_nums[index])
if verbose:
print("Case " + str(case_nums[index]+1) + ": " + str(caseValue))
# Simulate a simple game that is played to the end (pick a random case)
def SimulateGame():
possible = [0,1,5,10,25,50,75,100,200,300,400,500,750,1000,5000,10000,25000,50000,75000,100000,200000,300000,400000,500000,750000,1000000]
index = random.randint(0, len(possible)-1)
return possible[index]
# Simulate a simple game that is played to the end numGames number of times.
def SimulateGames(numGames=1):
# We can either open 25 cases, or we can simply pick one random value
results = {}
possible = [0,1,5,10,25,50,75,100,200,300,400,500,750,1000,5000,10000,25000,50000,75000,100000,200000,300000,400000,500000,750000,1000000]
for item in possible:
results[item] = 0
for _ in range(numGames):
current_game = Cases()
results[current_game.OpenCase(random.randint(0,25))] += 1
total = 0
for x in results:
total += x*results[x]
print("Average: " + str(total/numGames))
return results
# Returns a list of the simulated games through n rounds
def SimulatePartialGames(numGames, numRounds):
results = []
if numRounds > 10:
# Max of 10 rounds
numRounds = 10
num_cases = 0
for index in range(1,numRounds+1):
num_cases += max(1,7-index)
for _ in range(numGames):
current_game = Cases()
current_game.OpenRandomCases(num_cases)
current_game.round = numRounds
current_game.current_offer = (0.09*numRounds + 0.148)*current_game.GetMean()
results.append(current_game)
return results
# Calculates a semi-random offer for a given round
# The offer is based on the actual game data.
def GetOffer(current_round, board_average):
# Offer percentages hard coded based on 25% and 75% of offer percent of average in data
offer_percentage = {1: (0.11,0.21),
2: (0.22,0.35),
3: (0.31, 0.47),
4: (0.42, 0.65),
5: (0.53, 0.77),
6: (0.66, 0.86),
7: (0.80, 0.98),
8: (0.89, 1.08),
9: (0.986, 1.099)}
offer_range = offer_percentage[current_round]
offer = ((offer_range[1] - offer_range[0]) * abs(np.random.normal()) + offer_range[0])*board_average
return offer
# Allows the player to play a game
def PlayGame():
round = 1
done = False
cases = Cases()
while(not done):
cases_to_open = max(1,7-round)
print("Round " + str(round) + " =============================")
print("Remaining Cases: " + str(cases.RemainingCases()))
case_list = ast.literal_eval(input("Open " + str(cases_to_open) + " cases (list): "))
for index in range(cases_to_open):
current_case = case_list[index]
cases.OpenCase(current_case,verbose=True)
if round == 10:
print("You won " + str(list(cases.cases.values())[0]))
done = True
else:
# Calculate the offer
offer = GetOffer(round,cases.GetMean())
print("Remaining Amounts: " + str(cases.RemainingAmounts()))
decision = input("Offer: " + str(offer) + " (y/n): ")
if decision == "y":
done = True
round += 1
# Returns games where the median is greater than or equal to the target
def SimulateTargetMedian(numGames, numRounds, targetMedian):
result = []
while len(result) < numGames:
current_game = SimulatePartialGames(1, numRounds)
if len(current_game) > 0 and current_game[0].GetMedian() > targetMedian:
result.append(current_game[0])
return result
# Our heuristic. Should we accept the offer or continue
def ShouldContinue(offer,game):
if offer > 140000 and game.GetLargeProb(offer) >= 0.5:
should_continue = False
elif (len(game.RemainingCases()) % 2 == 1): #and (min(offer,game.GetMedian())/max(offer,game.GetMedian()) < 0.95):
should_continue = (offer > game.GetMedian())
else:
should_continue = True
return should_continue
# Simulate Games with basic decision making
# Starting at round 6, we apply our heuristic (ShouldContinue)
def SimulateOfferAnalysis(numGames):
results = []
for _ in range(numGames):
result = SimulatePartialGames(1,6)
game = result[0]
done = False
current_round = 6
while not done:
offer = GetOffer(current_round,game.GetMean())
if not ShouldContinue(offer, game):
done = True
win_amount = int(offer)
results.append(win_amount)
else:
current_round += 1
# open a random case
game.OpenRandomCases(num=1)
if current_round == 10:
done = True
win_amount = list(game.cases.values())[0]
return results
# Simple test of 10 games to the current round
# This is used to debug the heuristic
def test(current_round):
result = SimulatePartialGames(10, current_round)
for game in result:
offer = int(GetOffer(current_round, game.GetMean()))
print(game.RemainingAmounts(), offer, ShouldContinue(offer,game))



