When I learned imaginary numbers in school, I saw no value in them. I learned when to create them, but for the remainder of my academic career, I never needed them again, so I never sought to understand the purpose. However, recently, I discovered the Mandelbrot set.


These beautiful images were created using complex numbers (in case you want to know the more practical reason for complex numbers, see here).
In this post, I will give just enough background on the math of complex numbers to create a mandelbrot OSL shader and then we will walk through the shader code itself.
The math
The math is actually fairly simple. The equation we will use is:
z = z^2+c
Where c is a complex number. Now, before you freak out and leave this page, our use of complex numbers is extremely simple.
As a reminder, a complex number is created whenever we need to take the sqrt(-1). We represent a complex number as a real number and an imaginary number.
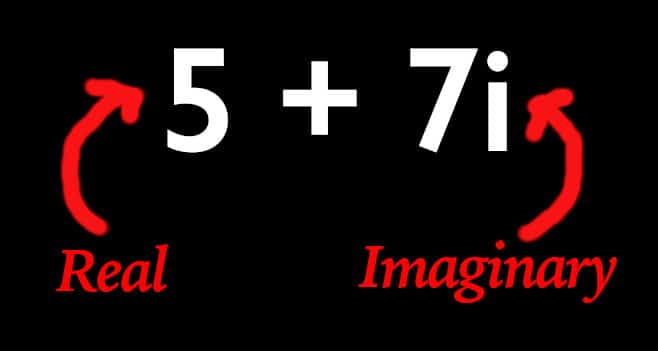
Operations on Complex Numbers
Going back to our equation:
z = z^2+c
We see that we need to be able to multiple and add complex numbers. I definitely had to refresh my memory on complex number operations.
We start with addition, because it is easy. You simply add real + real and imaginary + imaginary.
Multiplication is slightly more difficult. The complex number is a binomial (polynomial that is the sum of two terms. Therefore, we need to use the FOIL method (First, Outside, Inside, Last). For example:
(2+3i)*(5+3i) = 1 + 21i
First: 2*5=10
Outside: 2*3i = 6i
Inside: 3i*5 = 15i
Last: 3i*3i = 9i^2
We group the terms: 10 + 21i + 9i^2
We simplify, remember that i is equivalent to sqrt(-1). Therefore, i^2 is equal to sqrt(-1)^2 = -1. In our case, 9i^2 becomes -9.
This results in: 1+21i.
As a side note, in the course of creating this post, I learned that Python has built-in capabilities for complex number math. Before I posted the example above, I double checked my math in Python.

Mandelbrot Set Math
With that refresher on complex number operations, we can now complete two iterations of our equation:
z = z^2+c
We will use c = 2+3i
In this case:
z = 0 + c = 2+3i
In the next iteration, we calculate
z = (2+3i)^2 + 2+3i = -5+12i + 2 + 3i = -3 + 15i
Feel free to check me on my math.
Absolute Value
The last math concept we need to know is absolute value of a complex number. To get this, we simply square the real number, square the coefficient of the imaginary number, add them together and take the square root.
Using z = -3 + 15i from above:
abs(z) = sqrt((-3)^2 + (15)^2) = sqrt(9 + 225) = 15.30
There is No Escape … From the Mandelbrot Set
Now that we know the basic math of complex numbers, how do we use the equation z = z^2 + c?
If we are texturing a flat plane, we will use the x coordinate as our real number and the y coordinate as the imaginary number. For example, the position (3,7) would be 3+7i. For this equation, we want to determine how many iterations of our equation z=z^2 + c does it take for the abs(z) to exceed 2. If the number of iterations exceeds a MAX number, then we shade it one color. If we reach 2 before MAX, then we shade it another color.
Easy? Let’s move on to the shader.
On to the Shader
Before we implement the Open Shading Language shader, why are we using OSL for this texture? There are two reasons. First, although nodes can handle math, it requires a lot of nodes. Each operation requires a separate node. You can manage through node groups, but it is still more complicated than code. Second, and maybe even more important is iterations. We don’t know how many times we will run the equation. The number of iterations depends on whether the complex number leads to a result that is greater than 2. Nodes are not great whenever we need iterations. For those two reasons, we will use Open Shading Language. If you need a quick refresher on Open Shading Language, see our previous post, How to Use Open Shading Language in Blender.
The code is actually quite simple. We will break it into three parts:
- Handling complex numbers
- Mandelbrot function
- The Shader
For a full copy of the code, see our Github repository.
Handling Complex Numbers in Open Shading Language
To handle complex numbers in Open Shading Language, we will use a structure (struct) for the number itself and then three functions for the math operations.
First, we will create a structure. Open Shading Language allows structures (see OSL Specification 5.9). I wish you could create a class in OSL; however, the structure and functions we create are fairly close.
Our structure is very simple. We have two float fields. One will keep the real number. The other will keep the imaginary number.
struct complex
{
float real;
float imaginary;
};Complex Number Operations
Next, we will create functions to handle the complex number addition and multiplication. OSL allows us to override the add and multiply operators (see OSL Specification 6.4.3). This is really useful to keep our code clean.
complex __operator__add__ (complex a, complex b)
{
complex final;
final.real = a.real + b.real;
final.imaginary = a.imaginary + b.imaginary;
return final;
}
complex __operator__mul__ (complex a, complex b)
{
complex final;
final.real = a.real * b.real + a.imaginary * b.imaginary * -1;
final.imaginary = a.real * b.imaginary + a.imaginary * b.real;
return final;
}The addition operator is easy. We simply create a new complex number. We add the input real numbers and input imaginary numbers. We return the final result.
Multiplication is a little more complicated. To create the real number, we multiply the real numbers of the inputs. We also multiply the coefficients of the imaginary numbers and multiply this part by -1 (see above for the reason). We add these two together. Next, we multiply and then add the outside and inside factors (see FOIL above). We then return the result.
We also created a function to handle a variable power in the equation. This function has its limits. It only operates on integer powers (i.e., 0, 1, 2, 3). A future enhancement will be to allow non-integer powers.
complex pow(complex a, int degree)
{
if(degree == 0){
return {1,0};
} else if (degree < 1){
return a;
}
complex final = {1,0};
for(int index=0; index < degree; index++){
final = final * a;
}
return final;
}The final math operation is the absolute value. We square both the real and imaginary parts of the number, add, and then take the square root of the sum.
float absolute(complex a)
{
return sqrt(pow(a.real,2)+pow(a.imaginary,2));
}The Mandelbrot Function
Next, we move on to the Mandelbrot function.
float mandelbrot(complex c, int degree, int max_iter)
{
complex z = {0,0};
int n = 0;
while((absolute(z) <= 2.0) && (n<max_iter)){
z = pow(z,degree)+c;
n += 1;
}
return float(n)/max_iter;
}The function takes three parameters:
- C: the complex number
- degree: the power of the Mandelbrot function to use
- max_iter: the maximum number of iterations to perform before concluding that the complex number did not escape
The function sets initial values of 0 for Z and n. The function then enters a while loop that checks that the absolute value of Z is less than 2 and the number of iterations has not exceed max_iter.
The core of the loop is simply the Mandelbrot equation. Remember to also increment n, otherwise, you may end up with an infinite loop.
The function returns n/max_iter. If n hit max_iter, this will result in a return value of 1. Otherwise, the number will be between 0 and (max_iter-1)/max_iter.
The Shader
The shader is easy to implement. Input parameters represent the majority of the code:
shader mandelbrot(vector pos=P,
color inputColor1 = color(1.0),
color inputColor2 = color(0.0),
float scale = 1.0,
int degree = 2,
int max_iterations = 256,
output color out_color = color(0.0, 0.0, 0.0),
output float result = 0.0)
{
// Create an imaginary number
complex input = {pos[1]/scale,pos[2]/scale};
result = mandelbrot(input,degree,max_iterations);
out_color = mix(inputColor1,inputColor2, result);
}Inputs
We start the shader code with six inputs:
- pos: the current point we are shading
- inputColor1 and inputColor2: colors used to shade the output
- scale: the amount by which to divide the input
- degree: the highest power we use in the Mandelbrot equation
- max_iterations: the max number of iterations we run before we decide that the complex number did not escape
Outputs
The shader has two outputs:
- outputColor: uses the input colors to shade the texture based on whether the complex number escaped or not
- result: the number of iterations that were run divided by the max_interations
Shader Body
The function starts by converting the current position into a complex number. Next, we send that complex number into the Mandelbrot function. As noted above, the result is the number of iterations that the function ran divided by the max_iterations. This leads to a number between 0 and 1.
The final step in the shader is to color based on the result. We use the OSL mix function, which is a linear blending. The function takes three inputs, two colors to mix and a factor by which to mix.
Results
Below are some of the results of our shader. As noted above, in the future, I am interested in looking at non-integer powers. I also want to better understand how to “zoom into the boundary” to create the infinite zoom.



Additional Resources
Below are additional websites that I used as resources in developing this post:




